Exact Solvers for TSPN-Variants
Engineering exact solvers for Traveling Salesman Problems with Neighborhoods (TSPN) and related problems through the gain and exploitation of theoretical insights.
Under Construction
This page shall in the near future show my research agenda for the Traveling Salesman Problem with Neighborhoods (TSPN) and related problems. We already made some progress in this area, and are optimistic that we can soon publish our results, with many more ideas to follow.
Traveling Salesman Problem with Neighborhoods
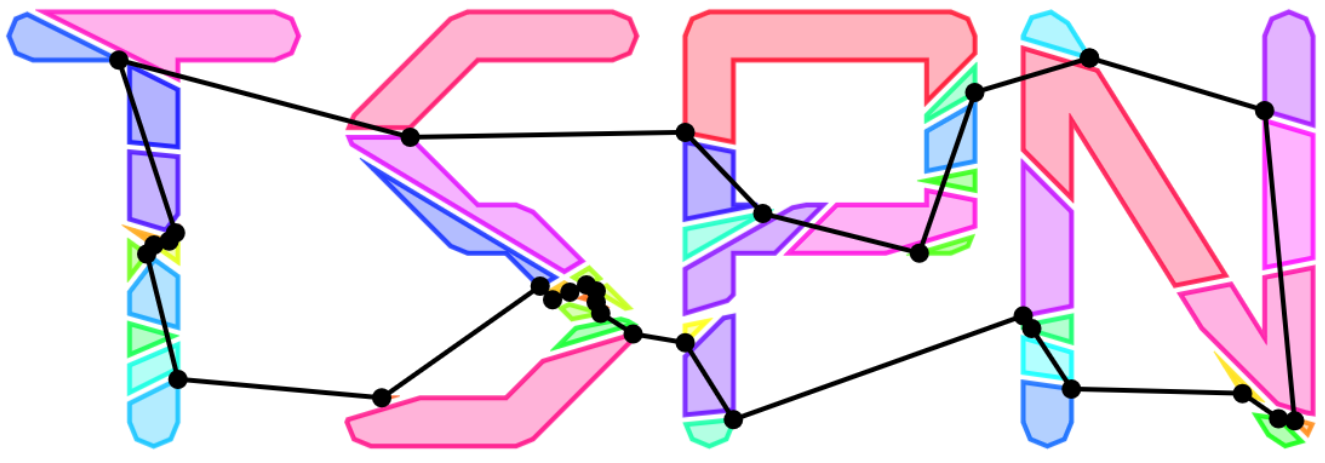
The Traveling Salesman Problem with Neighborhoods (TSPN) extends the classical Traveling Salesman Problem (TSP) by allowing visits to any point within specified regions, or “neighborhoods,” instead of fixed points. This nuanced change has significant implications for real-world applications, particularly in robotics, logistics, and manufacturing where flexibility in routes can lead to cost savings and efficiency improvements. TSPN models better capture spatial flexibility, making the problem more aligned with real-world constraints and thus more valuable for generating practical solutions.
We developed a branch-and-bound algorithm that utilizes the fact that for a given sequence of convex polygons, the optimal tour can be computed in polynomial time via a Second Order Cone Program (SOCP). To efficiently compute the optimal solution for an unknown sequence of non-convex polygons, we need to cleverly branch on the sequence and on convex partitions of the polygons.
We already have a prototype and an initial study for an SOCP-based solver. Next we will finish the development and perform a thorough study of its performance.
Similarly, we will develop a solver based on sampling and GTSP, and will compare the two approaches.
Close-Enough TSP
The Close-Enough TSP is a special case of the TSPN where the neighborhoods are disks of a given radius. The goal is to find a tour that visits every disk. This problem is an important subroutine for computing coverage tours for robots, see the project Coverage Tours.
In our current research, we have developed a branch-and-bound algorithm that leverages a Second Order Cone Programming (SOCP) relaxation to find optimal solutions for the problem at hand. This refinement builds upon the foundational work by Courtion et al. (A branch-and-bound algorithm for the close-enough traveling salesman problem), offering enhanced performance and computational efficacy. While the SOCP relaxation is naturally extendable to scenarios involving convex polygons, its application to the Traveling Salesman Problem with Neighborhoods (TSPN) necessitates specialized branching and relaxation techniques to address the inherent non-convexity of the problem.
Beside having made some theoretical insights that help us to improve the algorithm, we are also exploiting parallelism to speed up the computation and the recent improvements of Gurobi’s SOCP-solver.

Another approach to solve the Close-Enough TSP is by sampling points in the disks and solving the problem as a Generalized Traveling Salesman Problem (GTSP). This idea was used, e.g., by Carrabs et al. (An adaptive heuristic approach to compute upper and lower bounds for the close-enough traveling salesman problem). By using a more adaptive sampling strategy, we are optimistic that this approach can be improved. Such a variant is also currently under development by us.
We already have a prototype for a more powerful version of the SOCP+BnB-based approach. We will finish this development and evaluate the performance.
We are currently developing a prototype for an improved version of the Sampling+GTSP-based approach. We will develop a complete solver and compare the performance of the different approaches.
We will look for more pruning rules, i.e., properties of optimal solutions.
We will look for better relaxations, which can help us with the lower bounds.
Close-Enough TSP with Obstacles
One interesting extension of the problem is the introduction of polygonal obstacles that the tour is not allowed to intersect. I want to explore this variant in the future. A convex partition or covering of the feasible region could be used in a Branch-and-Bound algorithm to enforce the non-intersection constraint.
We will develop a solver than can deal with obstacles. We will start with convex obstacles and then generalize.
Close-Enough TSP with Turn Costs
How does the Close Enough TSP behave with turn costs? In a preliminary investigation, we observed that this is significantly harder than the Close Enough TSP without turn costs. The first step would be to compute a tour for a given sequence of disks. In the best case, we want an optimal tour, but a good approximation would also be acceptable to continue. The optimal sequence could then be found via a Branch-and-Bound algorithm.
The GTSP-approach could also be used here, but it will require a more sophisticated sampling strategy to make sure that it converges to the optimal solution.
Can we efficiently compute optimal trajectories if the sequence of disks is known? Can we extend the approach to arbitrary linear combinations of distance and turn angles?
Can we build a BnB-algorithm comparable to the SOCP-based on without turn costs?
Develop a sampling based solver.
Large Neighborhood Search to scale up
Large Neighborhood Searches (LNS) are a powerful technique to optimize many combinatorial problems to near-optimality. A key component of LNS is the neighborhood structure, which defines the set of solutions that can be reached from a given solution by a single operation. For geometric problems, the geometry often gives you a lot of structure that can be exploited to define an effective neighborhood for LNS. We already utilized this approach in ESA 2023 and ALENEX 2024 with great success. I am planning to further explore this approach in the future and apply it to other geometric problems.
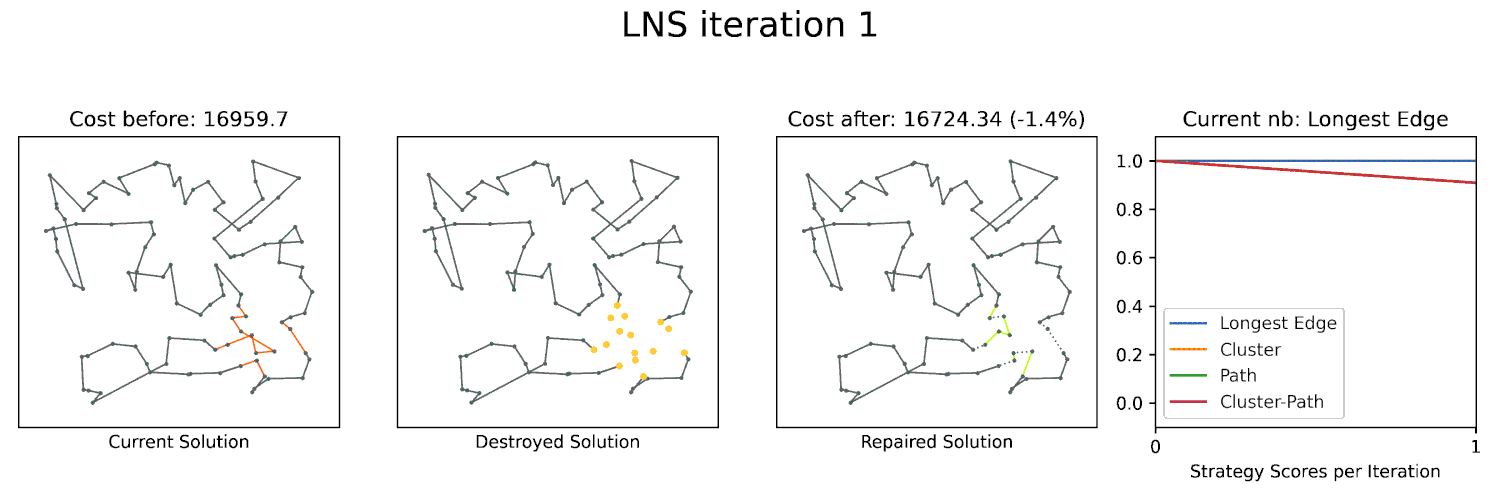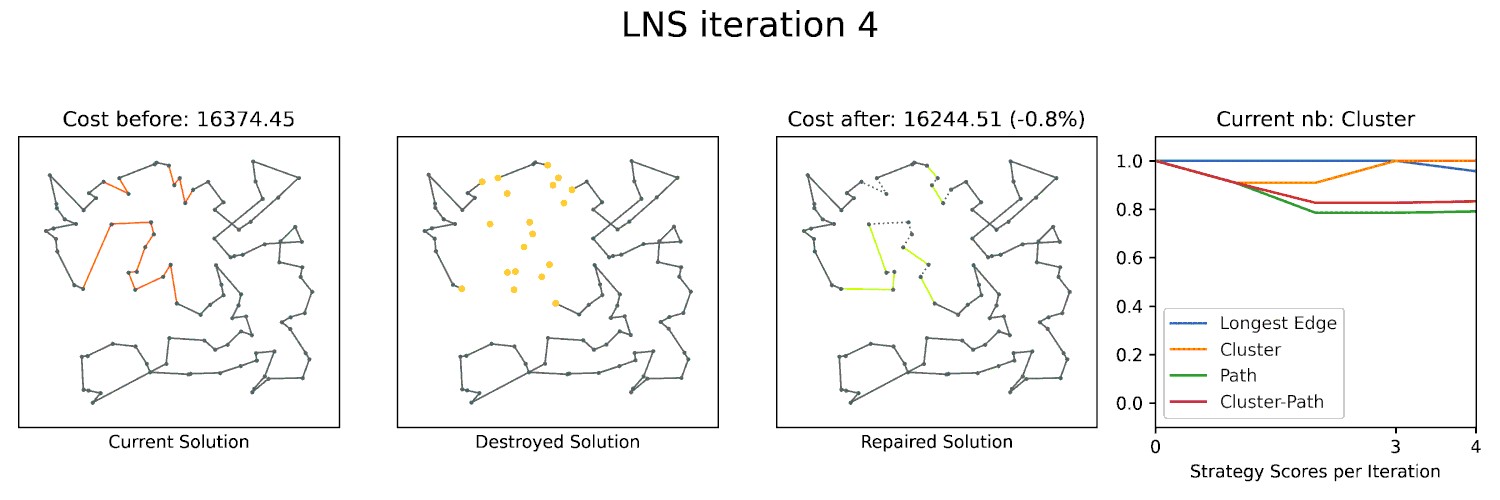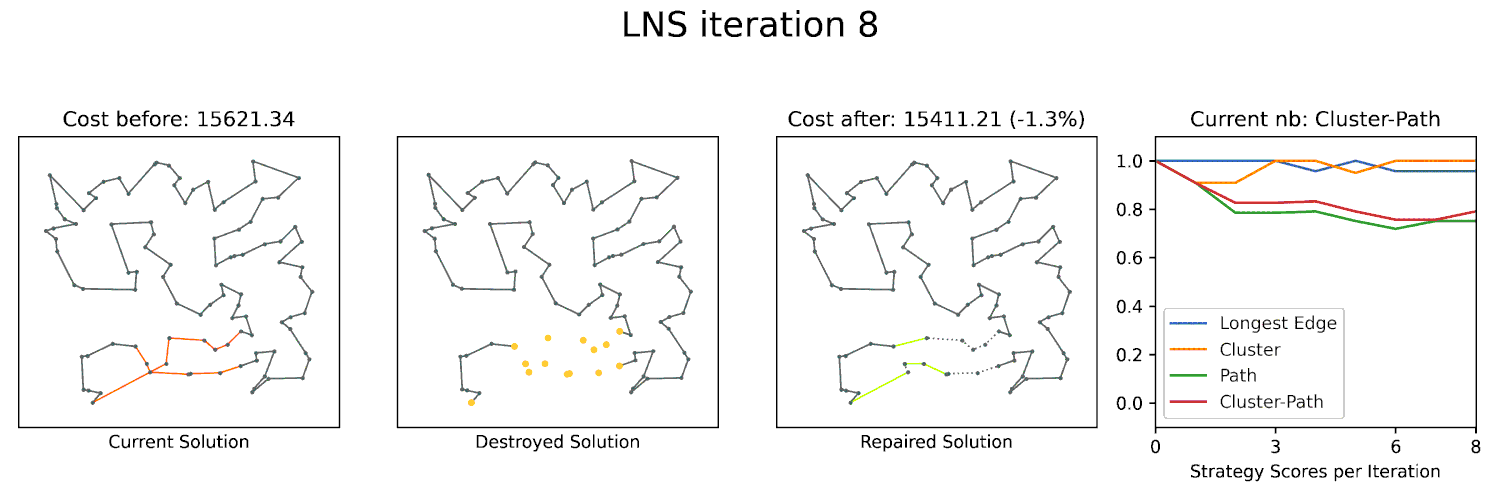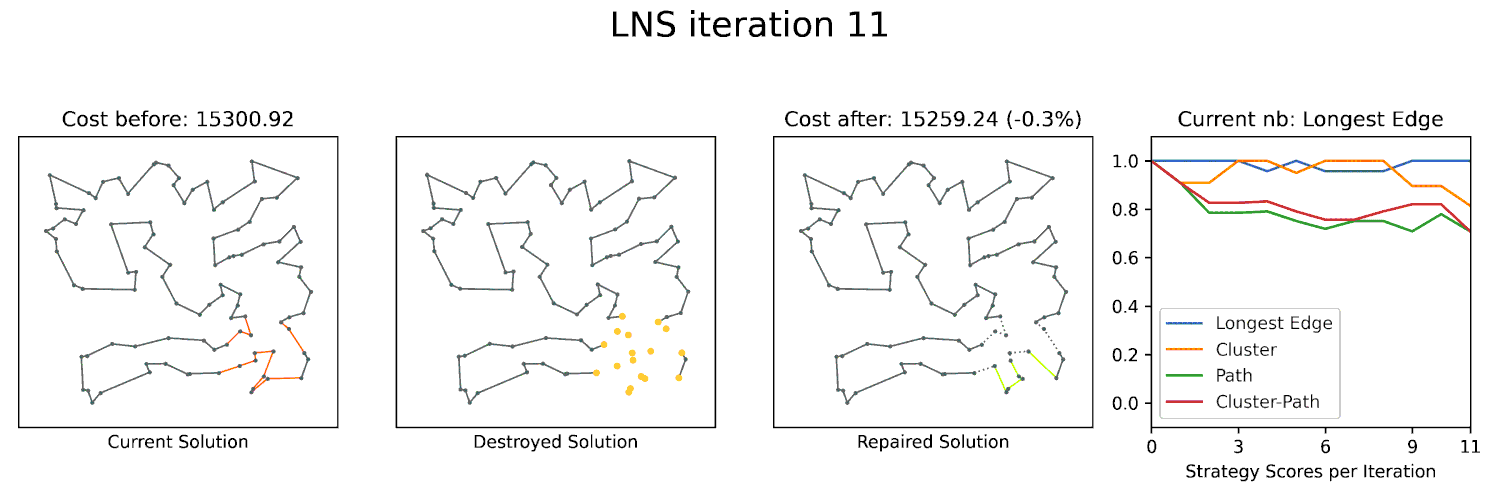
We will use the solvers above in a Large Neighborhood-based heuristic to compute good solutions for larger instances.