Coverage Tours (with Turn Costs)
The optimization of various geometric coverage tour problems with and without turn costs. This is my longest running project with already many publications but still a lot of open questions.
THIS TEXT IS STILL UNDER CONSTRUCTION
The Traveling Salesman Problem (TSP) stands as a prominent and extensively explored problem in combinatorial optimization. In the TSP, the goal is to determine the shortest possible route for a salesman who must visit a collection of cities and return to the start, optimizing for the least total distance traveled. Recognized as NP-hard, the TSP does not have an efficient algorithm for optimal solutions; however, through advanced algorithm engineering, it is now possible to solve relatively large instances to optimality.
Unlike the TSP, where the destinations are explicit points, many geometric touring problems require visiting areas or a collection of areas, rather than specific points. Furthermore, these problems often demand considerations beyond merely minimizing distance. Factors such as turn costs, which accrue when changing travel direction, become crucial in these scenarios.
In this project, I am delving into various geometric touring problems, encompassing scenarios both with and without turn costs. The aim is to extend our understanding and solution strategies beyond the classical TSP, accommodating the unique challenges posed by regional visits and additional cost factors.
TSP with Turn Costs in Grid Graphs
In addressing the challenge of covering a designated region, a common strategy is to transform the area into a grid graph and then apply the Traveling Salesman Problem (TSP) framework to it. While this approach might seem straightforward, it overlooks a significant aspect in many practical applications: turn costs. Turn costs are pivotal in activities such as lawn mowing, cleaning, painting, or surveillance, where the expense incurred in changing direction—owing to the need to decelerate, turn, and then accelerate again—is often significantly higher than moving straight. A relatable example is the extra effort involved in maneuvering a lawnmower at the end of each row while mowing a lawn.
This challenge, inherently NP-hard, was underscored in our investigation. The complexity of its cycle cover relaxation, a longstanding open question noted as Problem 53 in the Open Problems Project, was addressed in our work presented at (Fekete & Krupke, 2019). Here, we not only proved the NP-hardness of the problem but also developed a new approximation algorithm based on linear programming.

Further advancements in our research were showcased at (Fekete & Krupke, 2019), where we refined the algorithm for greater efficiency and implemented it in C++. Our experiments demonstrated an optimality gap of less than 10% for instances with tens of thousands of vertices. Additionally, our Integer Programming model significantly outperformed previous ones, allowing for the optimal solution of instances with up to 1000 vertices. We also extended our research to the prize-collecting variant of the problem, further enriching the scope of our study.
Partial Coverage Path Planning
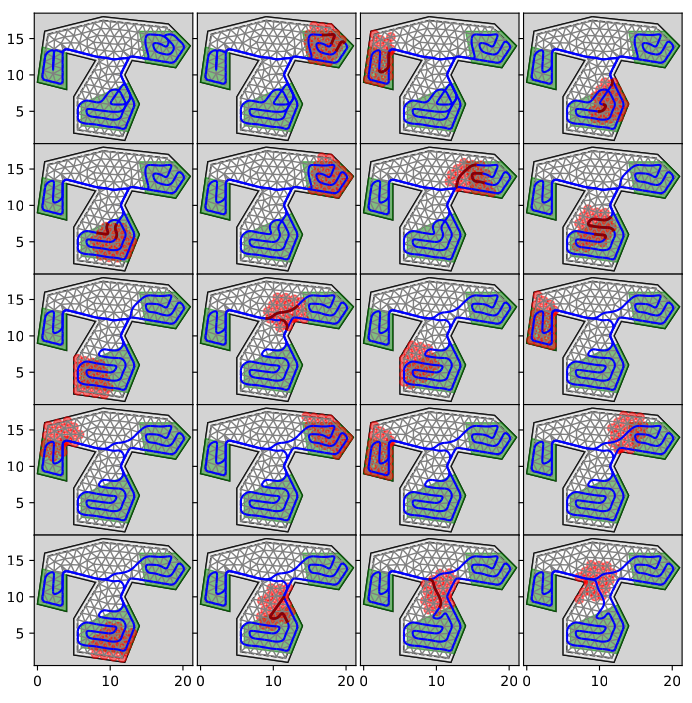
In this project, we focused on creating a coverage tour optimizer for environments with polygonal shapes, tailored to accommodate the specific movement dynamics of robots. A key aspect of our approach was the ability to allow partial coverage, particularly concentrating on areas of importance. The initial stage involved a methodical process of converting the targeted area into an optimal grid or mesh structure. This task was crucial for ensuring that the coverage paths devised were both efficient and effective.
Building on the foundations laid in the previous part, we extended the approximation algorithm designed for regular square grids to suit arbitrary mesh structures. This adaptation was not straightforward and required careful consideration of the unique challenges posed by non-uniform grids.
Further, we incorporated several additional optimizations to enhance the algorithm’s performance. These improvements were aimed at refining the coverage paths, making them more practical and efficient for real-world applications.
The result of this project is a comprehensive framework that not only optimizes coverage trajectories in polygonal environments but also does so with a solid theoretical basis. This framework represents a step forward in robotic coverage optimization, offering a solution that is both practically viable and theoretically sound. It demonstrates our ability to bridge the gap between complex theoretical algorithms and their practical implementation in dynamic, real-world scenarios.

We are looking into using a finer grid, e.g., halving the cell sizes. This would allow to just visit every second row and give some more flexibility to obtain better solutions, while still having the benefits of a discrete optimization environment. However, this can make the optimization significantly more difficult.
Lawn Mowing
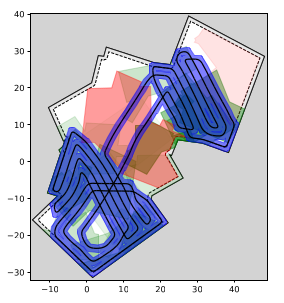
The Lawn Mowing Problem seeks to find the shortest tour that covers a given polygonal area using a circular tool. Unlike the previous problems, the movement of the tool is not constrained by the environment. Our primary focus lies in the computation of optimal solutions for small instances without any discretization.
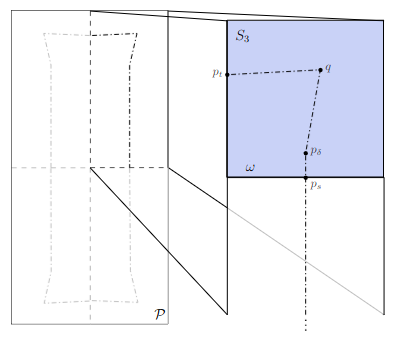
A key insight is that this problem can be viewed as a specific instance of the Close-Enough Traveling Salesman Problem (CE-TSP) with an infinite set of unit disks. Leveraging existing CE-TSP solvers, we have successfully calculated the first provable optimal solutions for very small instances of the Lawn Mowing Problem.
In our ongoing project, Exact Solvers with TSPN-Variants), we are dedicated to developing more efficient CE-TSP solvers tailored to this problem and already made some notable progress. These advancements will enable us to compute optimal solutions for moderately larger instances, allowing us to study the structure of the problem deeper and develop better heuristics for larger instances.
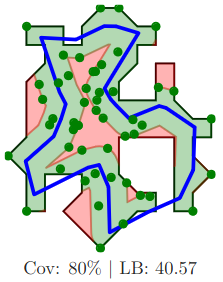
How can we compute optimal or near-optimal tours for larger instances of the Lawn Mowing Problem?
Can we use a combination of the Puzzle Solver (for an initial trajectory) and the CE-TSP-based Solver (to fine-tune the trajectory via LNS) to compute high quality solutions for medium-sized instances?
Lawn Mowing with Turn Costs
Once we have a good algorithm for the Close-Enough TSP with turn costs, we can apply it to the lawn mowing problem. The goal is to find optimal or near-optimal tours for lawn mowing with turn costs on small instances. This can then be used to understand more about the structure of the problem and develop heuristics for larger instances.
How can we compute optimal or near-optimal tours for small instances of the Lawn Mowing Problem with Turn Costs?
Milling (Lawn Mowing with Obstacles)
A further question is the computation of optimal tours for the Milling Problem, where the tool is not allowed to intersect with obstacles. This problem is significantly more difficult to solve, but we have some ideas on how to approach it.
How can we compute optimal or near-optimal tours for small instances of the Milling Problem? As a first steps, we will look into how to do it for the Lawn Mowing Problem with convex obstacles.
Large Neighborhood Search for Geometric Problems
Large Neighborhood Searches (LNS) are a powerful technique to optimize many combinatorial problems to near-optimality. A key component of LNS is the neighborhood structure, which defines the set of solutions that can be reached from a given solution by a single operation. For geometric problems, the geometry often gives you a lot of structure that can be exploited to define an effective neighborhood for LNS. We already utilized this approach in ESA 2023 and ALENEX 2024 with great success. I am planning to further explore this approach in the future and apply it to other geometric problems.
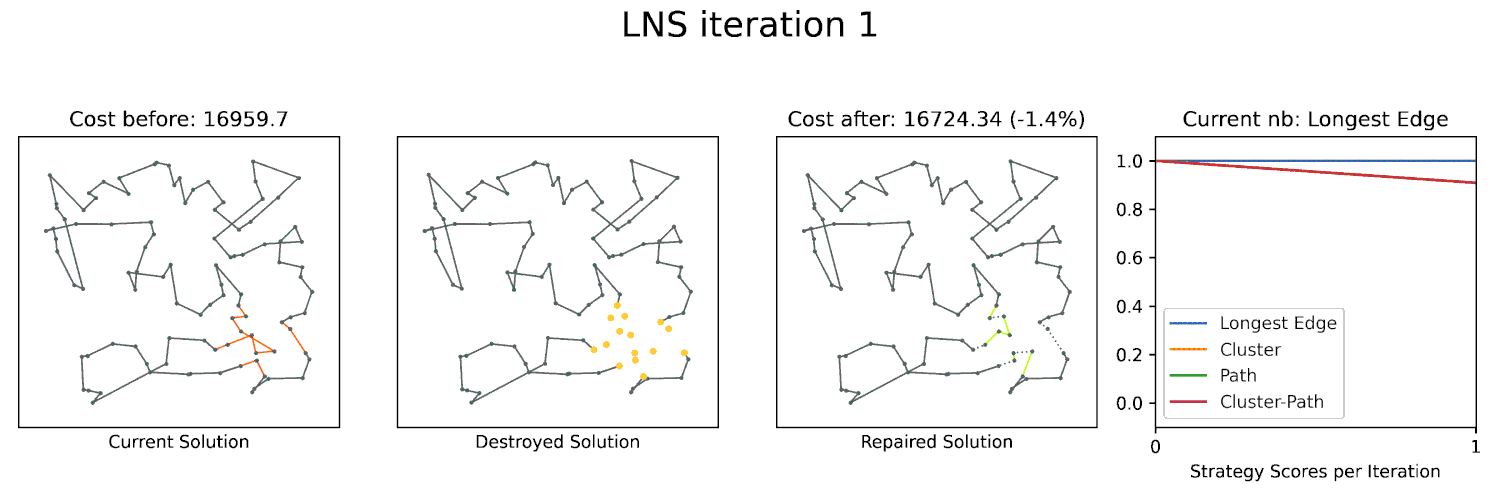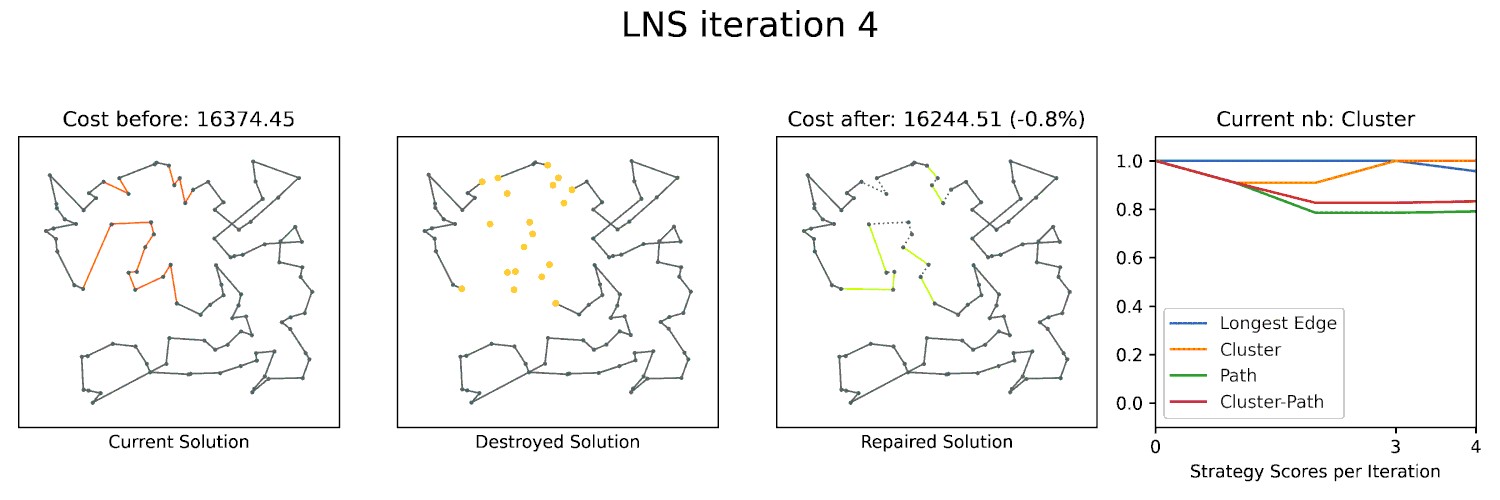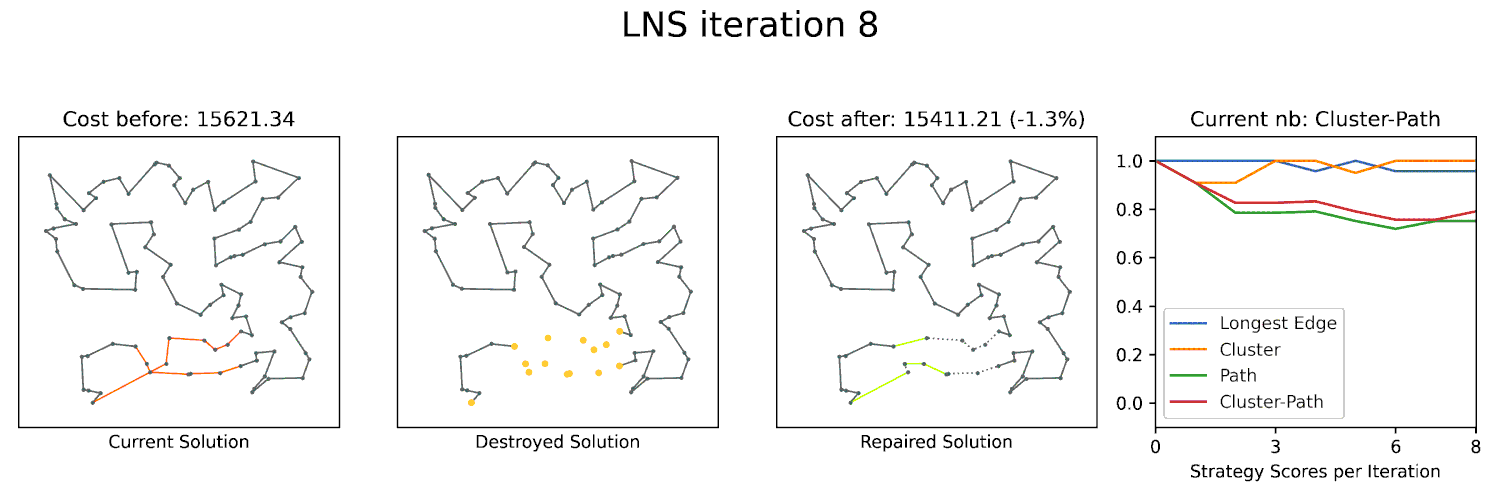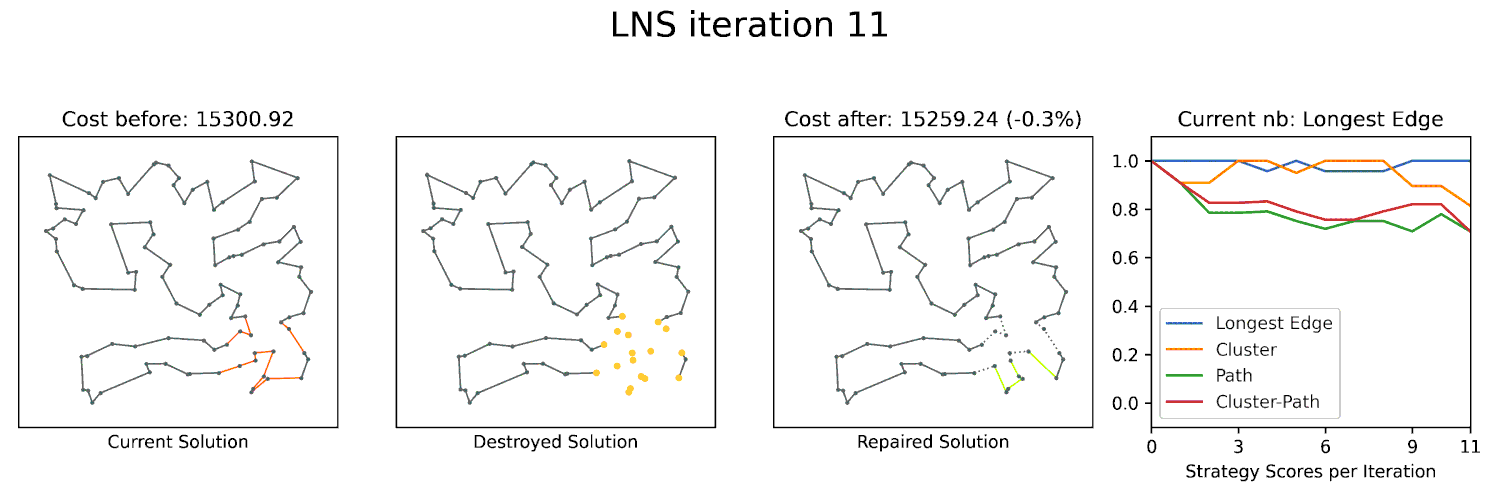
Can we exploit the geometry of these problems to engineer powerful optimizers based on Large Neighborhood Search? Our (near-)optimal solvers would be a key element for such a technique.
Publications
2024
-
 Near-Optimal Coverage Path Planning with Turn CostsIn 2024 Proceedings of the Symposium on Algorithm Engineering and Experiments (ALENEX) , 2024
Near-Optimal Coverage Path Planning with Turn CostsIn 2024 Proceedings of the Symposium on Algorithm Engineering and Experiments (ALENEX) , 2024
2023
-
 A Closer Cut: Computing Near-Optimal Lawn Mowing ToursIn 2023 Proceedings of the Symposium on Algorithm Engineering and Experiments (ALENEX) , 2023
A Closer Cut: Computing Near-Optimal Lawn Mowing ToursIn 2023 Proceedings of the Symposium on Algorithm Engineering and Experiments (ALENEX) , 2023 -
 The Lawn Mowing Problem: From Algebra to AlgorithmsIn 31st Annual European Symposium on Algorithms (ESA 2023) , 2023
The Lawn Mowing Problem: From Algebra to AlgorithmsIn 31st Annual European Symposium on Algorithms (ESA 2023) , 2023
2019
-
 Covering Tours and Cycle Covers with Turn Costs: Hardness and ApproximationIn Algorithms and Complexity - 11th International Conference, CIAC 2019, Rome, Italy, May 27-29, 2019, Proceedings , 2019
Covering Tours and Cycle Covers with Turn Costs: Hardness and ApproximationIn Algorithms and Complexity - 11th International Conference, CIAC 2019, Rome, Italy, May 27-29, 2019, Proceedings , 2019 -
 Practical Methods for Computing Large Covering Tours and Cycle Covers with Turn CostIn Proceedings of the Twenty-First Workshop on Algorithm Engineering and Experiments, ALENEX 2019, San Diego, CA, USA, January 7-8, 2019 , 2019
Practical Methods for Computing Large Covering Tours and Cycle Covers with Turn CostIn Proceedings of the Twenty-First Workshop on Algorithm Engineering and Experiments, ALENEX 2019, San Diego, CA, USA, January 7-8, 2019 , 2019